
The higher the statistical power of a test, the lower the risk of making a Type II error. Power is the probability of avoiding a Type II error. Type II error : you conclude that spending 10 minutes in nature daily doesn’t affect stress when it actually does.Type I error: you conclude that spending 10 minutes in nature daily reduces stress when it actually doesn’t.Type II error: not rejecting the null hypothesis of no effect when it is actually false.

Type I error: rejecting the null hypothesis of no effect when it is actually true.There’s always a risk of making one of two decision errors when interpreting study results: Alternative hypothesis: Spending 10 minutes daily outdoors in a natural environment will reduce symptoms of stress in recent college graduates.Null hypothesis: Spending 10 minutes daily outdoors in a natural environment has no effect on stress in recent college graduates.
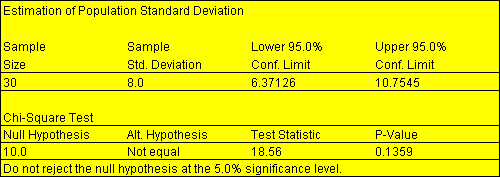
You rephrase this into a null and alternative hypothesis. Example: Null and alternative hypothesesYour research question concerns whether spending time outside in nature can curb stress in college graduates. The goal is to collect enough data from a sample to statistically test whether you can reasonably reject the null hypothesis in favor of the alternative hypothesis. In hypothesis testing, you start with a null hypothesis of no effect and an alternative hypothesis of a true effect (your actual research prediction). Having enough statistical power is necessary to draw accurate conclusions about a population using sample data.

Frequently asked questions about statistical power.


 0 kommentar(er)
0 kommentar(er)
